
Hence, the coordinates of \(x\) are _,_.Īns: The point \(P\) is at \(-3\) units from \(X\)-axis, and the \(y\) and \(z\)-coordinates are zero. The \(x\)-coordinate and the \(y\)-coordinate of the point \(S\) are _ and _, respectively. Hence, the coordinates of \(L\) are _,_.Ĥ.
The \(x\)-coordinate and the \(y\)-coordinate of the point \(L\) are _ and _, respectively. Hence, the coordinates of \(M\) are _,_.ģ. The \(x\)-coordinate and the \(y\)-coordinate of the point \(M\) are _ and _, respectively. Hence, the coordinates of \(B\) are _,_.Ģ. The abscissa and the ordinate of the point \(B\) are _ and _, respectively. See the figure given below and complete the following statements:ġ. The distance from the pole is called the radial distance or simply radius and the angular coordinate, polar angle.Ĭonsider the figure below that shows the relationship between polar and cartesian coordinates. Thus, a point in the polar coordinate system is represented as a pair of coordinates \((r,\,\theta )\). The point will have a unique distance from the origin \(r\). The angle \(\theta \) with the polar axis has a single line through the pole measured anti-clockwise from the axis to the line. Basically, we have two parameters, namely angle and radius. The polar coordinate system is a different way to express points in a plane.
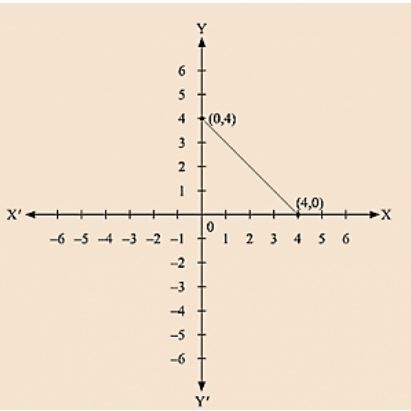
The \(y\)-coordinate of a point is its perpendicular distance from the \(X\)-axis measured along the \(Y\)-axis, and it is known as ordinate. The \(x\)-coordinate of a point is its perpendicular distance from the \(Y\)-axis measured along the \(X\)-axis, and it is known as abscissa.


 0 kommentar(er)
0 kommentar(er)
